Sooftware NLP - Attention Mechanism (어텐션 메커니즘)

본 포스팅을 이해하기 위해서는 다음 글에 대한 이해가 선행되는 것이 좋습니다.

• RNN (Recurrent Neural Network)
• LSTM & GRU (Long Short Term Memory & Gated Recurrent Unit)
• Seq2seq (sequence to sequence)

---

Seq2seq의 한계

기본적인 Seq2seq 모델은 간단한 구조라는 장점이 있었지만, 크게 2가지의 문제점이 존재한다.

1. 하나의 고정된 크기의 벡터에 모든 정보를 압축하다보니 정보 손실이 발생한다.
2. RNN의 고질적인 문제인 Vanishing Gradient Problem이 존재한다.

이러한 문제점들은 입력 데이터가 길어지면 성능이 크게 저하되는 현상으로 이어지게 된다. 이를 위한 기법으로 입력 데이터가 길어지더라도, 정확도가 떨어지는 것을 보정해주기 위해 등장한 방법이 어텐션(Attention) 기법이다.

Seq2seq의 문제점

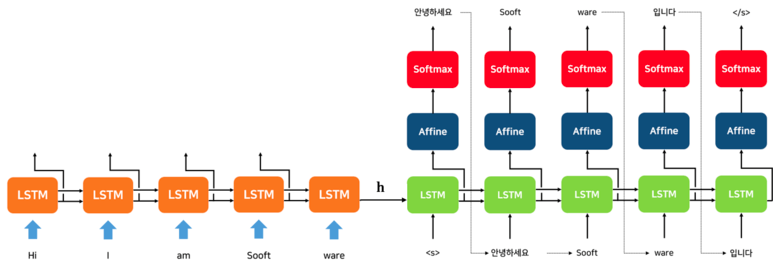
그렇다면 Seq2seq 구조에서 어떤 부분이 문제였는지를 살펴보자. Seq2seq의 구조를 살펴보면, Encoder에서 계산한 여러 Hidden State 중 마지막 Hidden State만을 Decoder에서 사용하게 된다.

즉, 마지막 Encoder의 RNN 셀의 마지막 Hidden State를 제외하고는 사용되지 않는다.

어텐션 매커니즘은 바로 이 사용되지 않은 Hidden State를 이용한 아이디어이다.

어텐션의 기본 아이디어는 Decoder에서 출력 결과를 예측하는 매 시점(time step)마다, Encoder의 Hidden State를 다시 한 번 참고한다는 아이디어다.

그리고 이 참고하는 비율을, 해당 시점에서 예측해야하는 결과와 연관이 있는 부분을 판단하여 좀 더 집중 (Attention) 하여 본다고 하여 Attention Mechanism이라고 부른다.

Attention의 직관적인 설명

그렇다면 이 Attention Mechanism이 왜 효과가 있을지를 먼저 생각해보자.

위와 같은 영어 문제가 있다고 해보자. 우리는 위의 영어 문제를 해석할 때, 처음부터 끝까지 혹은, 처음부터 한 문장이 끝날 때까지 모두 읽고 해석한다면 해석하기 쉽지 않을 것이다.

이 보다는 위의 □ 부분과 같이 부분부분 끊어서 해석하는 편이 더 나은 결과를 도출할 것이다.

Encoder of Seq2seq

그럼 다시 Seq2seq의 Encoder에 주목해보자. 시각별 RNN 셀의 Hidden State에는 당연히 직전에 입력된 단어에 대한 정보가 많이 포함되어 있을 것이다.

예를 들면 “Sooft”라는 단어가 들어간 RNN 셀의 Hidden State는 “Sooft”의 성분이 많이들어간 벡터라고 생각할 수 있다.

어텐션의 아이디어는 여기서 시작된다.

Attention Mechanism

위 그림은 디코더의 세 번째 RNN 셀에서 출력 단어를 예측할 때, 어텐션 매커니즘을 사용하는 모습이다. 그럼 어텐션 매커니즘이 어떻게 적용되는지를 살펴보자.

Attention Score

어텐션 매커니즘은 디코더에서 출력 결과를 예측할 때, 인코더의 Hidden State들을 다시 한 번 참고해주는 방법이라고 했다.

이 때 어느 인코더의 Hidden State를 얼마나 참고할지를 결정해야 한다.

이 때, 현재 예측에 필요한 정도라고 판단되는 점수를 어텐션 스코어 (Attention Score)라고 한다.

이러한 어텐션 스코어를 구하기 위해, 현 시점의 디코더의 Hidden State (s_t)와 인코더의 모든 Hidden State들과 각각 내적을 수행한다.

※ 벡터의 내적의 결과는 스칼라가 나온다 ※

Attention Distribution

앞에서 각 인코더와 디코더의 현재 Hidden State를 내적한 값은 스칼라로 나오기 때문에 이를 소프트맥스 함수를 적용해서 어텐션 분포를 구한다.

※ 소프트맥스 함수는 입력받는 값을 모두 0 ~ 1 사이의 값으로 정규화하며 총합은 항상 1이 된다 ※

이렇게 구한 어텐션 분포(Attention Distribution)는 각 인코더 Hidden State의 중요도라고 볼 수 있다.

Attention Distribution X Encoder Hidden State

소프트맥스를 통해 얻은 어텐션 분포를 각 인코더 Hidden State와 곱해준다.(Broadcasing)

Weight Sum

각 어텐션 분포와의 곱을 통해 얻어진 Hidden State들을 전부 더해준다. (element-wise)

이렇게 얻은 벡터를 인코더의 문맥을 포함하고 있다하여 컨텍스트 벡터(Context Vector)라고도 부른다.
기본적인 Seq2seq에서 Encoder의 마지막 Hidden State를 컨텍스트 벡터라고 부른 것과 대조된다.

• ※ 이해를 돕기 위한 예시 ※

Concatenating to s_t

그렇게 구한 컨텍스트 벡터와 현 시점의 디코더 셀의 Hidden State와 연결해준다. (여기서는 concatenate라는 방법을 사용했지만 평균을 내서 사용하는 방법도 있다)

그리고 이렇게 구한 벡터를 이용해서 최종 예측 값을 구하게 된다.

이상이 가장 기본적인 어텐션인 Dot-Product Attention의 설명이다.

어텐션 스코어를 구할 때 Dot-Product를 한다고 해서 Dot-Product Attention이라고 한다.

다양한 종류의 어텐션

어텐션은 그 효과가 검증된 만큼, 많은 종류의 기법이 존재한다. 하지만 다른 어텐션들과의 차이는 어텐션 스코어를 구하는 중간 수식의 차이일 뿐이지, 크게 개념을 벗어나지 않는다.

위의 표처럼 다양한 어텐션의 종류가 있으며, 어떤 어텐션을 적용하느냐도 모델의 성능을 좌우할 것이다.