Sooftware NLP - Beam Search (빔서치)

본 포스팅은 “빔서치”에 대한 본질적인 개념보다는 Encoder-Decoder 모델 (Seq2seq) 을 기반으로 한 모델에서 빔서치가 어떻게 적용되는지에 중점을 두었습니다.

본 포스팅을 이해하기 위해서는 다음 글에 대한 이해가 선행되는 것이 좋습니다.

• Seq2seq

Greedy Search

기본적인 Sequence to sequence (이하 Seq2seq) 모델에서의 디코딩 과정은 보통 Greedy Decoding 방식을 따른다.

Greedy Decoding이란 단순하게 해당 시점에서 가장 확률이 높은 후보를 선택하는 것이다. 시간복잡도 면에서는 훌륭한 방법이지만, 최종 정확도 관점에서는 좋지 못한 방법이다.

특정 시점 t에서의 확률 분포 상에서 상위 1등과 2등의 확률 차이가 작든 크든, Greedy Decoding 방식은 무조건 가장 큰 놈에게만 관심이 있을 뿐이다.
(1등과 2등의 차이가 정말 미묘하다면, 2등이 정답일 경우도 고려해주어야 할 것이다)

이러한 예측에서 한 번이라도 틀린 예측이 나오게 된다면, 이전 예측이 중요한 디코딩 방식에서는 치명적인 문제가 된다.

Beam Search

Greedy Decoding의 이러한 단점을 “어느 정도” 극복하기 위해 나온 방법이다.

가장 좋은 방법은 나올 수 있는 모든 경우의 수를 고려한 뒤 누적 확률이 가장 높은 한 경우를 선택하는 것이겠지만, 이는 시간복잡도 면에서 사실상 불가능한 방법이다.

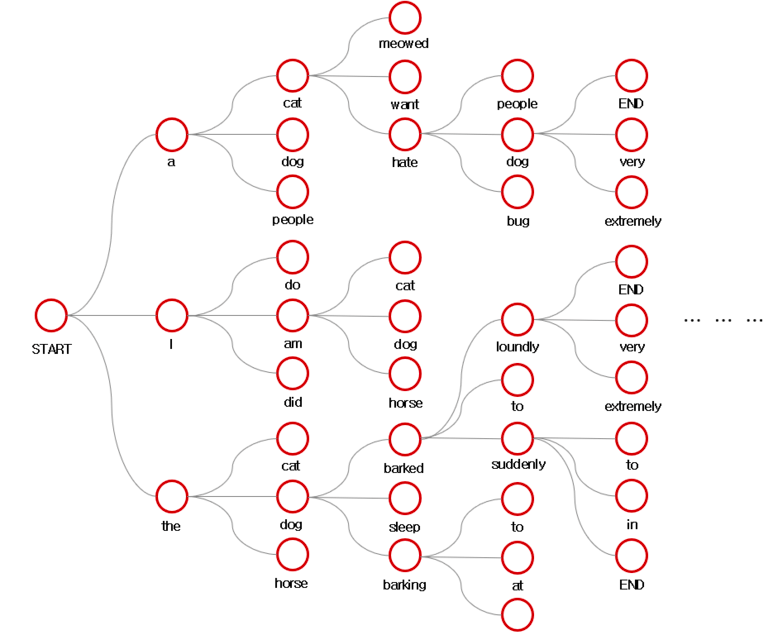
빔서치는 이러한 Greedy Decoding과 모든 경우의 수를 고려하는 방법의 타협점이다. 해당 시점에서 유망한 빔의 개수만큼 (이하 K) 골라서 진행하는 방식이다. 그럼 이제 어떤 방식으로 진행이 되는지를 살펴보자. ( K = 3 )

Start

START 토큰이 입력된다.

Step 1

START 입력을 바탕으로 나온 예측 값의 확률 분포 중 가장 높은 확률 K개를 고른다.

(이제부터 이 K개의 갈래는 각각 하나의 빔이 됩니다)

Step 2

K개의 빔에서 각각 다음 예측 값의 확률 분포 중 가장 높은 K개를 고른다.

( 이를 자식 노드라고 하겠습니다 )

Step 3

총 K²개의 자식 노드 중 누적 확률 순으로 상위 K개를 뽑는다.

• ※ 주의 사항 ※

빔서치에서 고려하는 모든 확률은 누적 확률입니다. 어떠한 자식 노드들이 서로 같은 확률을 가지더라도, 어떤 빔에서 뻗어나왔냐에 따라 누적 확률은 달라지게 됩니다.

Step 4

뽑힌 상위 K개의 자식노드를 새로운 빔으로, 다시 상위 K개의 자식 노드를 만든다.

Step 5

EOS를 만난 빔이 K개가 될 때까지 Step3 - Step4를 반복한다.

이상이 빔서치의 전반적인 과정이다.

EOS(End Of Sentence) Token

위에서 살펴본 빔서치에서 각각의 빔은 EOS를 만날 때까지 Step1 ~ Step5의 과정을 진행한다.
그럼 어떠한 빔이 EOS를 만났을 때는 어떤 과정이 일어나는지를 살펴보자.

위의 그림처럼 어떤 빔이 EOS (or END) 를 만나게 되면 해당 빔은 최종 선택 후보에 오르게 된다.

그리고, 끝난 빔의 자리를 대신하여, 해당 시점에서 상위 K개에 밀려서 K+1위를 차지했던 빔이 활성화 되어서 이후 K개의 빔을 유지한다.

( 어떤 시점에서 x개의 빔이 EOS를 만나서 종료된다면, 상위 K+1위 ~ K+x위의 빔이 활성화된다 )

그렇게 EOS를 만난 빔이 K개가 될 때까지 진행하고, EOS를 만난 빔이 K개가 된다면, 총 K개의 후보 중에서 가장 높은 누적 확률을 가진 빔을 최종적으로 선택한다.

Length Penalty

마지막으로 누적 확률 계산시에 필요한 Length Penalty를 살펴보자. 확률의 범위는 0.0 ~ 1.0이다. 이는 누적하여 곱할수록, 크기가 점점 작아진다는 것을 의미한다.

그렇다면, 당연히 빔의 길이가 길어질수록 누적 확률의 값이 작아지는 것은 당연할 것이다. 이러한 길이에 따른 불공평을 해소하기 위해 Length Penalty라는 개념이 나오게 된다.

간단한 공식으로 길이가 길어짐으로 인해 발생하는 불공평성을 해결해주는 것이다. 보통 알파는 1.2 정도의 값을 사용한다고 한다. 위의 공식에서는 바로 5로 들어가 있지만, minimum length로 이것 역시 설정 가능한 파라미터이다.

파이썬 코드로는 다음과 같이 간단하게 구현할 수 있다.

위의 코드로 나온 결과값으로 현재 빔의 누적 확률을 나눠주면 된다.

new_prob = prob ÷ length_penalty 

Beam Search의 성능

Beam Search와 Greedy Decoding의 차이점은 단지 Greedy Decoding은 K=1인 Beam Search라는 것이다.

그러므로 당연히 더 많은 경우의 수를 고려해주므로, 예측 결과 역시 좋아지는 경우가 많다.

위는 빔 크기가 커짐에 따라 표현이 더욱 풍부해진 것을 확인할 수 있는 표이다. 실제로 빔서치를 적용하면 기계 번역에서 BLEU 성능이 2 가량 올라간다고 한다.

기계번역 뿐만 아니라, 본인이 음성 인식 대회에 참여했을 당시에 상위권 팀들 모두 입 모아서 빔서치를 적용했을 때 성능이 가장 많이 올랐다고 할 정도로 빔서치의 적용 여부는 NLP 모델의 성능에 크게 기여한다고 볼 수 있다.

다만 빔서치의 단점이라면, 기존 Greedy Decoding에 비해 코드로 구현하여 적용하기가 어렵다는 점이다.