Sooftware NLP - LSTM & GRU

본 포스팅을 이해가기 위해서는 아래 글에 대한 이해가 선행되는 것이 좋습니다.

• RNN (Recurrent Neural Network)

LSTM 등장 배경

RNN은 순환 경로를 포함하여 과거의 정보를 기억할 수 있었다.
구조가 단순하다는 장점이 있지만, 성능이 좋지 못하다는 단점도 존재한다.

이러한 단점의 원인은 많은 경우에 시계열 데이터에서 시간적으로 많이 떨어진
장기 의존 관계(Long Term)를 잘 학습할 수 없다는 데 있다.

여기서 “장기 의존 관계”가 무엇인지 짚고 넘어가자.

Sooft는 그의 방에서 TV를 보고 있었다. Ware는 그의 방으로 들어갔다. 
그리고 Ware는 ?에게 '안녕'이라고 인사를 했다.

위의 예시를 보자. ?에 들어갈 단어는 ‘Sooft’이다.
위의 문제에 올바르게 답하려면, 앞의 “Sooft는” 이라는 정보를 기억해둬야 한다.

하지만 기본적인 RNN의 구조에서는 이러한 장기 의존 관계에 취약하다.

RNN의 문제점

그렇다면 왜 RNN은 이러한 장기 의존 관계에 대해서 약한 것일까?

이 점에 대해서는 RNN의 Backpropagation을 살펴보면 알 수 있다.
위의 그림과 같이 RNN에서의 Backpropagation은 RNN 계층이 과거 방향으로
시간을 거슬러 가면서 gradient를 전달하게 된다.

하지만 이러한 기울기는 RNN 계층이 길어지게 되면 기울기가 작아지게 된다.
이를 Vanishing Gradient Problem(기울기 소실)이라고 한다.

그럼 RNN 계층에서 왜 Vanishing Gradient이 일어나는 원인을 살펴보자.

위는 RNN 셀의 구조이다.

위의 구조 중 ‘tanh’에만 주목해보자.
tanh와 dtanh의 그래프 모양은 다음과 같다.

여기서 우리는 gradient에 관심이 있으므로, dtanh에 주목해보면
dtanh 값은 항상 0~1 사이의 값인 것을 알 수 있다.

이는 역전파에서 gradient가 tanh 노드를 지날 때마다 값이 계속 작아진다는 의미이다.
tanh를 T번 통과하게 되면 gradient도 T번 반복해서 작아지게 된다.
그렇기 때문에 RNN 계층이 길어지게 되면 Vanishing Gradient Problem이 발생하게 된다.

Long Short Term Memory (LSTM)

이제 이러한 Vanishing Gradient를 일으키지 않는다는 LSTM의 구조에 대해 살펴보자.

위 그림은 RNN과 LSTM의 인터페이스를 비교한 그림이다.

인터페이스만 보더라도 LSTM 계층에는 c라는 경로가 추가된 것을 알 수 있다.

이 c를 기억 셀^{memory cell}이라 하며, LSTM의 전용 기억 매커니즘이다.

기억 셀의 특징은 데이터를 LSTM 계층 내에서만 주고 받고, 다른 계층으로는 출력하지 않는다는 것이다.
즉, 이는 LSTM도 내부적으로만 다르지 사용하는 입장에서는 RNN과 같은 인터페이스를 갖는다.

이제 LSTM의 구조를 차분히 살펴보자.
앞서 이야기한 것처럼, LSTM에는 기억 셀 c_t가 있다.
이 c_t에는 시각 t에서의 LSTM의 메모리가 저장되어 있는데, 과거로부터 시각 t까지에 필요한
메모리가 저장되어 있다고 가정하자.

그리고 필요한 정보를 모두 간직한 이 메모리를 바탕으로 외부 계층에 Hidden State h_t를 출력한다.
이때 출력하는 h_t는 다음 그림과 같이 기억 셀의 값은 tanh 함수로 변환한 값이다.
(여기서의 tanh는 각 요소에 tanh 함수를 적용한다는 뜻이다.)

여기서의 핵심은 3개의 입력 (x_t, h_t-1, c_t-1)를 이용하여 구한 c_t를 사용해
Hidden State h_t를 계산한다는 것이다.

※ LSTM 구조의 핵심은 ht는 단기상태 (Short Term) ct는 장기 상태 (Long Term)라고 볼 수 있다. ※

게이트^gate

여기서 뒷 내용을 이해하기 위해 게이트의 개념에 대해 이해하고 넘어가자.
게이트는 데이터의 흐름을 제어한다.

위의 그림처럼 물의 흐름을 제어하는 것이 게이트의 역할이다.

위의 그림처럼 LSTM에서의 게이트는 ‘열기/닫기’ 뿐 아니라, 어느 정도 열지를 조절할 수 있다.
그리고 이 열기 ~ 닫기 까지의 정도를 0.0 ~ 1.0의 실수로 표현할 수 있다.
그리고 이 0.0 ~ 1.0의 값이 다음으로 넘어갈 데이터의 양을 결정한다 !!

여기서 중요한 점은 ‘게이트를 얼마나 열지’라는 것도 데이터로부터 자동으로 학습된다는 점이다.

그리고 여기서 0.0 ~ 1.0이라는 범위에 주목해보자.
우리는 이러한 범위를 가지는 매우 좋은 함수를 알고있다.

바로 Sigmoid 함수이다.

Sigmoid 함수를 이용하면 어떤 값을 넣더라도 0.0 ~ 1.0의 값을 가질 수 있다.
그렇기 때문에 LSTM의 게이트에서는 tanh가 아닌 Sigmoid 함수를 사용한다.

LSTM의 Output 게이트

다시 LSTM 이야기로 돌아와보자.
게이트 얘기를 하기 전에 Hidden State h_t는 기억 셀 c_t에 단순히 tanh 함수를 적용한것 뿐이라고 했다.

그럼 방금 배운 게이트의 개념을 tanh(c_t)에 적용하는 것을 생각해보자.
즉, tanh(c_t)의 각 원소가 ‘다음 시각의 Hidden State에 얼마나 중요한가’를 조정해보자.

output 게이트의 열림 상태의 계산식은 다음과 같다.

위의 식을 보게되면 RNN 계층의 내부 계산에서 tanh가 아닌 Sigmoid를
사용했다는 점만 다르다는 것을 확인할 수 있다.

다음은 tanh(c_t)에 Output게이트를 추가한 모습이다.
output 게이트에서 수행하는 식은 σ로 표시했다.

그리고 이 σ의 출력을 o라고 한다면, h_t는 다음과 같이 계산된다.

여기서의 ⊙는 Hardmard Product (아다마르 곱) 이라고 하여, 행렬의 원소별 곱셈을 의미한다.

LSTM의 forget 게이트

다음으로 할 일은 잊을건 잊어버리는 것이다.
굳이 필요없는 정보를 계속 들고갈 필요는 없다.
그러므로 기억 셀에 ‘무엇을 잊을까’를 지시하는 것이다.
여기에도 앞의 게이트 개념을 사용한다.

전 층에서 넘어온 기억셀 c_t-1에 대해서 불필요한 개념을 잊게 해주는
게이트를 forget 게이트라고 한다.

여기서도 위의 Output 게이트와 마찬가지로 다음 식을 수행한다.

Output게이트의 식과 동일한 것을 확인할 수 있다.
여기서도 마찬가지로, forget게이트의 출력인 f와 이전 기억 셀 c_t-1의 아다마르 곱으로 계산한다.

LSTM의 새로운 기억 셀

forget 게이트를 거치면서 이전 시각의 기억 셀로부터 잊어야 할 기억이 삭제됐다.
이제는 새로 들어온 데이터로부터 정보를 추가해야한다.
그러기 위해서 위의 그림과 같이 tanh 노드를 추가한다.

이 때, Sigmoid가 아닌 tanh 노드를 추가하는 이유는 이 ‘새로운 기억 셀’은 게이트가 아닌,
새로운 데이터를 기억 셀에 추가하는 것이기 때문이다.

이제 이렇게해서 잊는 것 뿐만이 아닌, 새로운 정보까지 추가가 되었다.

LSTM의 input 게이트

마지막으로 새로운 정보가 들어있는 g에 게이트를 하나 추가할 생각이다.
앞에서 새로운 데이터에 대해서 추가를 했으니, 이 데이터를 얼마나 반영할지도 판단하는 것이다.
즉, 새로운 정보를 무비판적으로 수용하기보다는 적절히 취사선택하는 것이 이 게이트의 역할이다.

Output 게이트, forget와 동일한 식을 계산한다.
이후 똑같이 아다마르 곱을 통해 기억 셀에 추가해준다.

이상이 LSTM 계층 내에서 이뤄지는 처리이다.

LSTM의 계산그래프

앞에서까지 살펴본 LSTM의 계산그래프와 내부 연산은 위의 그림과 같다.
RNN에 비해 훨씬 복잡한 구조인 것을 볼 수 있다.

그리고 위의 LSTM 계산그래프의 게이트를 구분해보면 다음과 같다.

위의 계산그래프를 이해하고 기억해둔다면,
LSTM에서 내부적으로 어떤 일이 일어나는지를 알 수 있을 것이다.

LSTM의 Gradient Flow

STM의 구조는 설명했지만, 이것이 어떤 원리로 Vanishing Gradient를 방지해주는 걸까?
그 원리는 기억 셀 c의 역전파에 주목하면 볼 수 있다.

위의 그림은 기억 셀에만 집중하여, 그 역전파의 흐름을 그린 것이다.
이때 기억 셀의 역전파에서는 ’+‘와 ‘X’ 노드만을 지나게 된다.
’+’ 노드는 Gradient를 그대로 흘릴 뿐이므로 남는 것은 ‘X’ 노드이다.

근데 여기서 중요한 점이 이 노드는 RNN과 같은 ‘행렬 곱’이 아닌 아다마르 곱을 계산한다.
그리고 RNN과 같이 똑같은 가중치 행렬을 사용하는게 아닌,
새로 들어온 데이터에 대해서 행렬곱을 수행하게 된다.

그러므로 매번 새로운 값와 행렬 곱이 되므로 곱셈의 효과가 누적되지 않아
Vanishing Gradient가 일어나기 어려운 구조인 것이다.

또한 여기서 ‘X’ 노드에 주목해보자.
이 ‘X’ 노드의 계산은 forget 게이트가 제어한다.

역전파 계산시 forget 게이트의 출력과 상류 gradient의 곱이 계산되므로,
forget 게이트가 ‘잊어야 한다’고 판단한 기억 셀의 원소에 대해서는
해당 기울기가 작아지고, ‘잊어서는 안 된다’고 판단한 원소에 대해서는
그 기울기가 약화되지 않은 채로 과거 방향으로 전해진다.
따라서 중요한 정보의 기울기는 소실 없이 전파된다.

Gated Recurrent Unit (GRU)

앞에서까지 LSTM에 대해 자세하게 설명했다.
LSTM은 아주 좋은 계층이지만, 매개변수가 많아서 계산이 오래 걸리는게 단점이다.

그래서 최근에는 LSTM을 대신할 변형된 RNN이 많이 제안되고 있다.
그 중 유명하고 그 성능이 검증된 GRU^{Gated Recurrent Unit}라는 RNN에 대해 알아보자.

( 여담으로, 이 GRU는 우리나라 ‘조경현’ 박사님이 제안한 구조이다. )

GRU는 LSTM의 게이트를 사용한다는 개념은 유지한 채, 매개변수를 줄여 계산시간을 줄여준다.
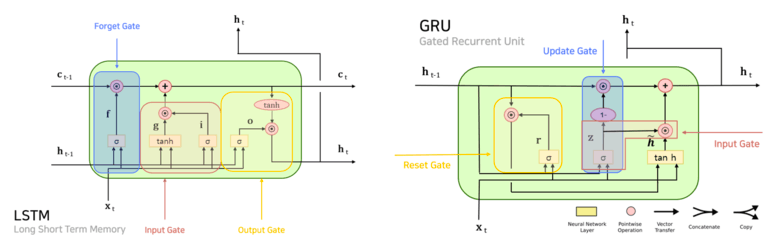
LSTM과 GRU의 인터페이스만 비교하더라도 둘의 차이점이 명확하게 드러난다.

그럼 GRU 내부에서 수행하는 계산을 살펴보자.

GRU에서 수행하는 계산은 이 4개의 식으로 표현된다.
위의 식만 보더라도 6개였던 LSTM에 비해 간단해진 것을 확인할 수 있다.
그리고 GRU의 계산 그래프는 다음 슬라이드의 그림과 같다.

앞의 LSTM에 비해 게이트의 수가 줄어든 것을 확인할 수 있다.
이처럼 GRU는 LSTM보다 계산 비용과 매개변수 수를 줄일 수 있다.

위의 그림처럼 GRU에는 기억 셀은 없고,
시간 방향으로 전파하는 것은 Hidden State인 h_t뿐이다.

그리고 r과 z라는 2개의 게이트를 사용한다.
여기서 r은 reset, z는 update 게이트이다.

reset 게이트 r은 과거의 은닉 상태를 얼마나 ‘무시’할지를 결정한다.
만약 r이 0이면

위의 식으로부터, 새로운 Hidden State는 입력 x_t만으로 결정된다.
과거의 Hidden State를 완전히 무시하는 것이다.

한편, Update 게이트는 Hidden State를 갱신하는 게이트이다.
LSTM의 forget 게이트와 input 게이트의 2가지 역할을 혼자 담당하는 것이다.

forget 게이트로써의 기능은 다음 식이 수행되는 부분이다.

과거의 Hidden State에서 잊어야 할 정보를 삭제한다.

그리고 input 게이트로서의 기능은 다음 식이 수행되는 부분이다.

새로 추가된 정보에 input 게이트의 가중치를 부여한다.

LSTM vs GRU

LSTM과 GRU 중 어느 쪽을 사용해야 하는지를 묻는다면,
주어진 문제와 하이퍼파라미터 설정에 따라 승자가 달라진다고 대답할 수 있다.

최근 연구에서는 LSTM이 많이 사용되지만, GRU도 꾸준히 인기를 끌고 있다.
GRU는 매개변수가 적고 계산량도 적기 때문에, 데이터셋이 작거나 모델 설계 시 반복 시도를 많이 해야 할 경우 특히 적합할 수 있다.