Page Rank

구글은 무엇을 기준으로 사이트를 보여주는 순서를 정할까요??

구글에 특정 단어를 검색하면 다음과 같이 여러 사이트 들을 보여주는 것을 알 수 있습니다.

구글은 이런 사이트들에 점수를 부여해주는데, 여기서 부여된 점수들을 Page Rank라고 부릅니다.

페이지 랭크를 부여하는 두 가지 원칙

1. 다른 여러 페이지에 링크가 많을 경우
2. 영향력있는 사이트에 링크되어 있는 경우

이 두가지 원칙을 따를 경우 점수가 높아진다!

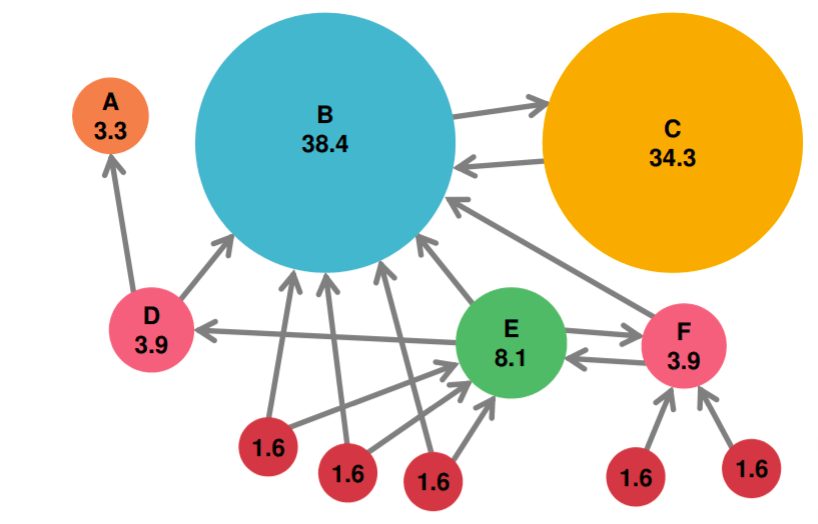
이 그림을 보시면 잘 이해가 되실 것 같아요.

원칙1에 의해 B사이트는 다른 여러 페이지들에게 링크가 많아 높은 점수를 부여 받은 것을 볼 수 있습니다. 또한 C사이트는 B사이트 단 하나만 링크됐지만 원칙2에 의해 높은 점수를 부여 받은 것을 볼 수 있습니다.

그렇다면 이런 원칙을 따르기 위해서 어떻게 점수를 부여하는지 알아봅시다.

예시로 4개의 각 사이트가 링크가 걸려있는 상황을 방향그래프로 나타내봤습니다.

이제 누군가 한 사이트에 접속 후 링크를 따라 계속 이동한다고 가정해봅시다.

최초 사이트1에서 이동을 한다면 링크가 하나밖에 없기 때문에 사이트2로 이동하게 되고 확률은 1이 됩니다.

다음으로 사이트2에서 이동을 한다면 링크가 총 3개가 존재하기 때문에 각 사이트로 갈 확률이 3분의1이 되겠죠.

이런 과정을 무한히 반복합니다.

그렇게 이런 과정을 계속 반복해서 각 사이트에 방문할 확률을 계산해보면, 놀랍게도 방문할 확률이 어떤 값에 수렴하게 됩니다.

즉 확률이 변하지 않는 순간이 오게 됩니다. 그리고 그 확률들을 바로 Page Rank라고 부릅니다.

그렇다면 t번 이동 시 각 사이트에 방문할 확률을 한번 구해봅시다.

먼저 처음 각 사이트에 방문할 확률을 임의로 정의해줍니다.

그리고 1번 이동 후의 각 사이트에 방문할 확률을 정의합니다.

1번 이동 후 사이트1에 방문할 확률을 계산한 식을 살펴보면,

1. 사이트1에서 사이트1로 방문할 방법이 존재하지 않기 때문에 a x 0
2. 사이트2에서 사이트1로 이동할 확률은 3분의 1이기 때문에 b x (1/3)
3. 사이트3에서 사이트1로 이동할 확률은 2분의 1이기 때문에 c x (1/2)
4. 사이트4에서 사이트1로 이동할 확률은 2분의 1이므로 d x (1/2)가 됩니다.

이렇게 모두 계산하면 최종적으로 다음과 같은 행렬이 하나 만들어지게 됩니다.

각 행이 동일한 변수를 사용하기 때문에 행렬곱 형태로 변환해 최종적으로 다음과 같은 식을 얻을 수 있습니다.

마찬가지로 동일한 논리에 따르면 2번 이동했을 때 각 사이트에 방문할 확률은 1번 이동했을 때의 상황에만 영향을 받게됩니다.

따라서 2번 이동했을 때의 행렬을 구해보면 다음과 같이 얻음을 알 수 있습니다.

자 이제 어느정도 반복되는 것을 알 수 있겠죠? 조금 더 직관적으로 볼 수 있도록 정의를 해봅시다.

고정된 사이트에 이동할 확률을 전이행렬 P, 그리고 각 사이트에 t번 방문할 확률을 X(t)로 정의하면 최종적으로

이렇게 깔끔하게 정리가 됩니다.

이 식을 이용해서 수렴된 각 사이트의 확률을 구하고 Page Rank값을 정의하는 것입니다.

검증

import numpy as np

P = np.array(
    [[0, 1 / 3, 1 / 2, 1 / 2],
     [1, 0, 0, 0],
     [0, 1 / 3, 0, 1 / 2],
     [0, 1 / 3, 1 / 2, 0]]
)

X = np.array([0.3, 0.2, 0.3, 0.2])

for idx, _ in enumerate(range(30)):
    X = P.dot(X)
    print("----", idx, "----")
    print(X)

마지막 식을 numpy라이브러리를 이용해 구현해봤습니다. 해당 코드를 실행하면

---- 15 ----
...
...
...
[0.29999997 0.30000007 0.20000074 0.19999922]
---- 16 ----
[0.3        0.29999997 0.19999963 0.20000039]
---- 17 ----
[0.3        0.3        0.20000019 0.19999981]
---- 18 ----
[0.3        0.3        0.1999999  0.20000009]
---- 19 ----
[0.3        0.3        0.20000005 0.19999995]
---- 20 ----
[0.3        0.3        0.19999998 0.20000002]
---- 21 ----
[0.3        0.3        0.20000001 0.19999999]
---- 22 ----
[0.3        0.3        0.19999999 0.20000001]
---- 23 ----
[0.3 0.3 0.2 0.2]
---- 24 ----
[0.3 0.3 0.2 0.2]
---- 25 ----
[0.3 0.3 0.2 0.2]
...
...
...

이런 결과값을 얻을 수 있는데, 23번째 연산부터 값이 수렴하는 것을 알 수 있습니다.

reference

• https://www.youtube.com/watch?v=PGeBhnHxg0E
• http://www.secmem.org/blog/2019/07/21/pagerank/