Sooftware NLP - RNN (Recurrent Neural Network)

본 포스팅을 이해하기 위해서는 피드포워드 네트워크에 대한 이해가 선행되는 것이 좋습니다.

RNN의 등장 배경

RNN에 대해 알아보기 전에 RNN이라는 놈이 왜 나왔는지 부터 생각해보자.

피드포워드 신경망의 문제점

피드포워드란 흐름이 단방향인 신경망을 뜻한다. 피드포워드 구조는 구성이 단순하여 구조를 이해하기 쉽고 많은 문제에 응용할 수 있다는 장점이 있지만, 커다란 단점이 하나 있으니 바로 시계열 데이터를 잘 다루지 못한다는 것이다. 즉, 단순한 피드포워드 신경망에서는 시계열 데이터의 성질(패턴)을 충분히 학습할 수 없다. 그래서 순환신경망^{Recurrent Neural Network(RNN)}이 등장하게 된다.

순환하는 신경망

RNN의 특징은 순환하는 경로 (닫힌 경로)가 있다는 것이다. 이 순환 경로를 따라 데이터는 끊임없이 순활할 수 있다. 그리고 데이터가 순환되기 때문에 과거의 정보를 기억하는 동시에 최신 데이터로 갱신될 수 있다.

위의 그림처럼 RNN 계층은 순환하는 경로를 포함한다.
이 순환 경로를 따라 데이터를 계층 안에서 순환시킬 수 있다.

여기서 Xt는 (X0, X1, …, Xt) 가 RNN 계층에 입력됨을 표현한 것이다.
그리고 그 입력에 대응하여 (h0, h1, …, ht) 가 출력된다.

순환 구조 펼치기

RNN의 순환 구조는 피드포워드 구조에서는 볼 수 없던 구조이지만, 이 순환 구조를 펼치면 친숙한 피드포워드와 유사한 신경망으로 변신시킬 수 있다. 위의 그림에서 보듯, RNN 계층의 순환 구조를 펼침으로써 오른쪽으로 진행하는 피드포워드 신경망과 비슷한 구조가 된 것을 볼 수 있다.

위의 그림에서 보듯, RNN 계층의 순환 구조를 펼침으로써 오른쪽으로 진행하는 피드포워드 신경망과 비슷한 구조가 된 것을 볼 수 있다.

하지만 RNN에서는 다수의 RNN 계층 모두가 실제로는 ‘같은 계층’인 것이 피드포워드 신경망과는 다르다.

위의 그림에서 알 수있듯, 각 시각의 RNN 계층은 그 계층으로의 입력과 그 전의 RNN 계층으로부터의 출력을 받는다.

그리고 이 두 정보를 바탕으로 현 시각의 출력을 계산한다. 이때 수행하는 계산 수식은 다음과 같다.

앞의 그림에서 보이듯이, RNN은 2개의 입력을 받는다. 그렇기에 각 입력에 대해 2개의 가중치가 있다. 하나는 입력 x를 출력 h로 변환하기 위한 가중치 W_x이고, 다른 하나는 1개의 RNN 출력을 다음 시각의 출력으로 변환하기 위한 가중치 W_h이다. 위의 식에서 행렬 곱을 계산하고 그 합을 tanh 함수를 이용해 변환한다.

즉, 이 식에서 볼 수 있듯이 현재의 출력 h_t는 한 시각 이전 출력 h_t-1에 기초해 계산됨을 알 수 있다.

이러한 구조를 갖고 있기에 RNN 계층을 메모리가 있는 계층이라고 한다.

RNN의 h는 상태를 기억해 시각이 1 스텝 진행될 때마다 위의 식 형태로 갱신된다.
이 h를 통상적으로 은닉 상태 (Hidden State) 혹은 은닉 상태 벡터 (Hidden State Vector)라고 한다.

위의 식이 어떻게 동작하는지를 자세히 살펴보기 전에 Hyperbolic tangent에 대해 살펴보고 가자.

Hyperbolic tangent

해당 부분은 http://taewan.kim/post/tanh_diff/ 을 참고했습니다.

Hyperbolic tangent 함수는 머신러닝에서 자주 사용되는 활성화 함수인 Sigmoid의 대체제로 사용될 수 있는 활성화 함수이다.

tanh는 sigmoid와 매우 유사한데, tanh와 sigmoid의 차이점은 sigmoid의 출력 범위가 0 ~ 1인 반면 tanh의 출력 범위는 -1 ~ +1 사이라는 점이다.

Sigmoid와 비교하여 tanh는 출력 범위가 더 넓고 경사면이 큰 범위가 더 크기 때문에 더 빠르게 수렴하여 학습하는 특성이 있다.

Hyperbolic tangent의 미분

RNN의 역전파를 계산하기 위해 필요한 tanh의 미분은 다음과 같다.

이후 RNN의 역전파 (Backpropagation) 에서 해당 수식이 사용된다.

RNN 계층의 순전파

앞에서 RNN 계층에서의 순전파에 사용되는 수식을 살펴봤다. 1개의 인풋 데이터에 대한 입력과, 한 시각 이전의 Hidden State가 입력된다는 점과 이를 tanh 함수에 넣는다는 점을 기억하자.

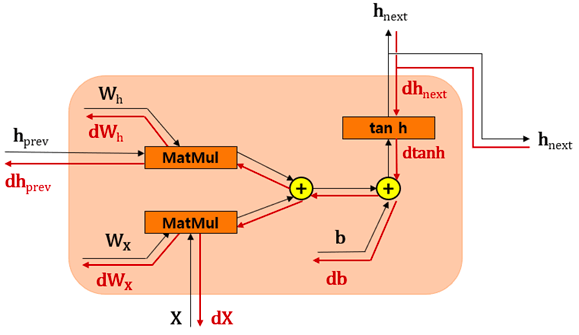
해당 수식을 시각화하여 표현하면 다음 그림과 같다.

X와 h_prev를 입력으로 받아 내부적인 계산을 거친 후, h_next라는 출력을 분기시켜 내놓는다.

다음 과정을 파이썬 코드로 표현하면 다음과 같다.

순전파는 위의 그림만 머리에 넣었다면 쉽게 이해할 수 있을 것이다. 그러면 이제 RNN에서의 역전파 (Backpropagation) 를 살펴보자.

BPTT (Backpropagation Through Time)

앞에서 봤듯이 RNN 계층은 가로로 펼친 신경망으로 간주할 수 있다. 따라서 RNN의 학습도 보통의 신경망과 같은 순서로 진행할 수 있다. 이를 그림으로 보면 다음과 같다.

위의 그림에서 보듯, 순환 구조를 펼친 후의 RNN에는 피드포워드 오차역전파법을 적용할 수 있다. 즉, 먼저 순전파를 진행하고 이어서 역전파를 수행하여 원하는 기울기^gradient를 구할 수 있다.

여기서의 오차역전파법은 ‘시간 방향’으로 펼친 신경망의 오차역전파법이라는 뜻으로 BPTT^{Backpropagation Through Time}이라고 한다.

이 BPTT를 이용하면 RNN을 학습할 수 있다. 하지만 위의 BPTT를 그대로 적용하게 되면 문제가 하나 있다.

바로 긴 시계열 데이터를 학습할 때 시계열 데이터의 크기가 커지는 것에 비례하여 BPTT가 소키하는 컴퓨팅 자원도 증가하기 때문이다. 또한 시간 크기가 커지면 역전파 시에 기울기 값이 조금씩 작아져서 0에 가까워지는 Vanishing Gradient Problem도 발생하게 된다.

Truncated BPTT

이러한 문제를 해결하기 위해 나온 방법이 Truncated BPTT이다. 시간축 방향으로 길어진 신경망을 적당한 지점에서 잘라내 여러 개로 만든다는 아이디어다. 그리고 이 잘라낸 작은 블록 단위로 오차역전파법을 수행한다. 이것이 Truncated BPTT라는 기법이다.

여기서 주의할 점은 역전파의 연결만 끊고, 순전파의 연결은 반드시 그대로 유지해야한다는 점이다. 즉, 순전파의 흐름은 끊어지지 않고 전파되어야 한다.

Backpropagation Review

이제 본격적인 RNN 계층의 역전파에 들어가기 전에, 기본적으로 필요한 역전파에 대한 개념을 간단히 살펴보자.

덧셈 노드의 역전파

덧셈 노드의 역전파는 상류에서 전해진 미분을 그대로 흘려보낸다.
z = x + y 라는 식이 있을 때 역전파를 생각해보면 다음과 같다.

σz/σx = 1, 
σz/σy = 1 

즉, 상류에서 전해진 미분에 x1 을 하는 것이므로 그대로 흘려보내는 것과 같다.

곱셈 노드의 역전파

곱셈 노드의 역전파는 상류의 값에 순전파 때의 입력 신호들을 ‘서로 바꾼 값’을 곱해서 하류로 보낸다. z = xy 라는 식의 역전파를 생각해보면 다음과 같다.

σz/σx = y, 
σz/σy = x 

전파 때의 입력신호들을 서로 바꾼 값이 되는 것을 확인할 수 있다. 그러므로 상류에서 들어온 신호에 순전파 때의 입력 신호들을 서로 바꾼 값을 곱해서 하류로 흘려보내면 된다.

여기서 그냥 곱셈인 경우와 행렬 곱셈은 다르지 않나? 라고 생각할 수 있는데, 행렬도 어차피 각 요소간의 곱으로 이루어진 집합이기 때문에 결과적으로는 같은 결과를 보인다.

Backpropagation in RNN

그럼 이제 본격적으로 RNN에서의 역전파를 살펴보자.

RNN 계층의 역전파 - (1) dh_next

먼저 다음 층의 역전파인 dhnext를 넘겨받는다. 피드포워드 신경망에서와 마찬가지로 순전파때의 반대 방향으로 역전파가 진행되는 점 주의

RNN 계층의 역전파 - (2) d_tanh

먼저 tanh의 미분결과가 1 - tanh2(x)이였던 점을 기억하자.
다음으로 위에서 흘러온 dh_next와 1 - tanh2(x)값을 곱해서 d_tanh를 계산한다.

RNN 계층의 역전파 - (3) 덧셈 노드

앞에서 간단히 살펴봤듯이 덧셈 노드의 경우 역전파를 그대로 흘려보낸다.
그러므로 db를 제외한 역전파는 dtanh를 그대로 흘려보내주면 되므로 따로 계산하지 않는다.
여기서는 미니배치 단위 학습을 고려해서 코드를 작성하므로 db는 NxH 형상을 가진다.
그러므로 편향 (b) 의 역전파는 데이터를 단위로 한 축인 axis=0의 합으로 계산한다.

RNN 계층의 역전파 - (4) 곱셈 노드

역시 앞에서 간단히 살펴봤듯이 곱셈 노드의 경우 상류에서 들어온 값에 순전파 때의 입력 신호들을 서로 바꾼 값을 곱해준다.
해당 법칙에 따라 나머지 모든 역전파를 계산한다.

Time RNN

앞에서까지는 하나의 RNN 계층에서 일어나는 순전파 및 역전파에 대해 살펴봤다.
이제 RNN 계층 T개를 연결한 신경망을 완성해보자.
이렇게 T개의 RNN을 연결한 신경망을 TimeRNN이라고 부를 것이다.
그리고 이 구현에서는 Truncated BPTT로 구현한다.

Time RNN의 순전파

순전파는 아래로부터 T개의 입력데이터인 xs를 입력으로 받는다.
미니배치 처리까지 고려했을 때의 xs의 형상은 NxTxD가 된다.
(N : 미니배치 수, T : 시계열 데이터 수, D : 입력벡터 차원 수)

앞에서 각 RNN 층에서의 순전파를 구현해놨기 때문에 이를 적당히 이어주기만 하면 된다.
Hidden State인 h는 처음 호출 시 영행렬로 초기화를 하고, 시계열 데이터의 수만큼 for문을 돌면서Hidden State를 업데이트 한다.
그리고 이 Hidden State T개의 집합인 hs를 반환한다.

Time RNN의 역전파

RNN은 순전파시에 출력이 2개로 분기되었던 점을 떠올리자.
이렇게 순전파시 분기한 경우, 역전파에서는 각 기울기가 합산되어야 한다.
따라서 역전파 시 RNN 계층에서는 기울기 (dh_t, dh_next)가 한산되어야 한다.

각 RNN 계층에서 역전파를 이미 구현해놨기 때문에 위 사항만 주의하여 적절하게 이어주면 된다.

추가적으로 주의할 점은 Truncated BPTT 방식이기 때문에 처음 dh는 0으로 시작된다는 점이다.

각 시각의 기울기인 dx를 모아서 dxs에 저장하고, 가중치 매개변수 역시 각 RNN 계층의 가중치 기울기를 합산하여 최종 결과를 멤버 변수 self.grads에 덮어쓴다.

이상으로 RNN의 등장배경부터 개념 및 순전파 역전파 등에 대해서 알아봤다.
다음에는 해당 RNN을 개선한 LSTM에 대해 알아보자.