AI & Speech Processing: DSP-2

본 글은 광운대학교 전자공학과 박호종 교수님의 강의를 듣고 작성되었음을 밝힙니다.

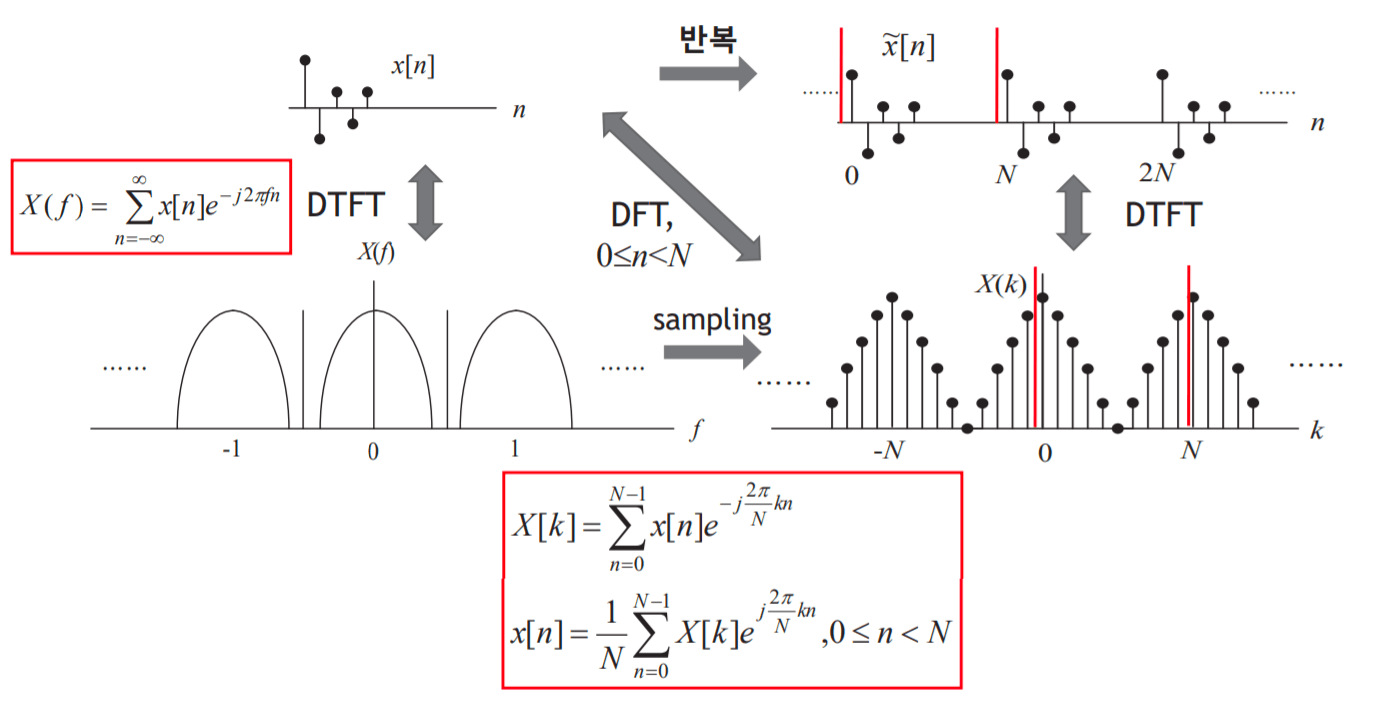
DFT (Discrete Fourier Transform)

Digital 처리를 위하여 time와 frequency domain에서 모두 sampling

f축에서 1 / N 간격으로 샘플링을 하게 되면 샘플한 결과는 주기마다 N개가 된다.
이때 샘플링을 했으므로 축은 f -> k로 변하게 된다.

이전 CTFT와 같이, 1 / N마다 샘플링을 하게 되면 반대 도메인에서 N마다 반복하게 된다.

• t축에서 샘플링을 했기 때문에 f축에서 반복이 일어난다. 또한 t축은 n축으로 변하게 된다.
• f축에서 샘플링을 했기 때문에 n축에서 반복이 일어난다. 또한 f축은 k축으로 변하게 된다.

사실 x[n]과 X(k)는 서로 연관이 있지 않다. x[n]은 X(f)와, x_hat[n]은 X(k)와 연관이 있을 뿐이다.
하지만 x[n]에서 X(k)로의 변환이 필요하니 조금 억지로나마 수학적으로 관계를 정의했다.
=> 이것을 DFT (Discrete Fourier Transform) 이라고 한다.

여기서 이렇게 변환이 가능하게한 트릭이 뭔지 살펴보자.
x[n]과 X(k)는 서로 관계가 없다. 하지만 어차피 일정 부분의 반복일 뿐이다.
그러므로, 반복되는 부분은 새로운 정보가 있지 않다. => 반복이 되는 내용만 알면 된다.

-N/2 ~ N/2 범위로 잡기보다는 보통 [0, N-1]을 범위로 잡는다고 한다.

그럼 Discrete Fourier Tansform 식을 한번 살펴보자.
x[n]식을 보게 되면, 1/N을 제외하고 보게 되면 아래와 같이 반복되는 모양이다.

여기서 1/N을 해주는 이유는 수학적 이론 때문이라고 한다.
(이는 그렇게 중요한 내용은 아니라고 넘어가셨다.)

여기서 중요한 부분은 0 ≤ n < N 부분이다.
위의 x_hat에 대해서 0 ≤ n < N으로 범위를 한정해주기 때문에 x[n]으로 변환될 수 있는것이다.

이렇게 조금은 억지로 x[n]과 X(k)의 관계를 정의할 수 있다.

※ 샘플링이 다른 도메인에서 반복이 되는 이유 ※

(a)와 같은 원 신호에 대해 샘플링을 한다는 것은 (b)와 같은 임펄스 신호와 곱셈을 한다고도 볼 수 있다.
그리고 시간 축에서의 곱셈은 주파수 축에서의 컨볼루션 연산과 같다.
( 반대로 주파수 축에서의 곱셈은 시간 축에서의 컨볼루션이다 )

그런데 (b)와 같은 임펄스 신호는 주기함수이기 때문에 주파수 대역에서 반복된다.
(주기함수는 cos(2nf + a)꼴이기 때문)

즉 임펄스 신호가 주파수 대역에서 주기적으로 반복되는 신호이기 때문에 이에 컨볼루션 연산을 취하게 되면, 주기적으로 반복하는 신호가 된다.

N-point DFT

이제 DFT에서 N에 주목해보자.
N은 주파수축에서는 1/N 마다 샘플링을 하고, 시간 축에서는 N을 주기로 반복하게 하는 중요한 파라미터다.

그럼 이러한 N은 어떤 점을 결정하게 될까?
아래 그림을 살펴보자.

만약 위와 같이 샘플링을 하게 되면 신호의 특성을 충분히 반영하지 못할 것이다.
즉, 신호에 담겨있는 많은 정보를 잃어버리게 된다.

이처럼 N은 주파수의 resolution을 결정한다. (음질)

촘촘하게 샘플링을 할 수록 더 좋은 음질 혹은 해상도를 가질 수 있게 한다.

위의 예제는 8kHz의 주파수 범위를 가지는 신호에 대해 100-Point 샘플링을 한 예이다.
이 때의 Spectral Resolution은 샘플링의 간격인 8k / 100 = 80Hz가 된다.

그리고 만약, 해당 신호에 대하여 200Hz의 low-pass filter를 통과시켰다고 해보자.
그럼 200Hz 이상의 신호를 지워버리면 된다.

근데 왜 98, 99신호가 남아있지? 라고 생각할 수 있다.

위의 그림을 봐보자. 우리는 [-N/2, N/2]를 범위로 하기보다는, 편의를 위해 [0, N-1]을 범위로 잡았다. 이때, 우리가 편의상 범위를 그렇게 잡았을 뿐이지, 원래 최고 주파수는 0.5 (가운데 )라는 사실을 기억해야한다.

0.5까지는 주파수가 증가하다가 0.5 이후로는 주파수가 감소한다는 사실을 꼭 기억해야한다.

즉, 가운데 (0.5) 를 기준으로 서로 대칭인 관계라는 사실을 꼭 기억해야한다.

LTI (Linear Time-Invariant) System

시스템에서 우리가 관심있는 것은 대표적으로 2가지이다.

1. 시스템 동작을 어떻게 구현할 것인가

2. 시스템의 성질이 무엇인가

충격응답 h[n]

충격응답을 넣었을 때 어떤 신호가 resonse로 나오는지가 관심이 있는 것이다.

위와 같이 조금은 복잡한 식이지만, 프로그래밍으로 구현한다면 충분히 구현이 가능하다.

하지만, h[n]만으로 이 시스템이 어떤 동작을 시키는 시스템이냐? 라는 질문에는 답하기 어렵다.

h[n]은 단지 수식으로 시스템의 동작만을 알려줄 뿐이다.

하지만 이러한 한계를 H(f) (주파수 응답) 을 이용하여 극복한다.

Y(f) = X(f)H(f)가 된다.
=> 시간 축에서의 컨볼루션은 주파수 축에서의 곱 !!

위와 같이 X라는 입력이 H라는 시스템에 들어갔을 때 어떤 식으로 변화가 이루어지는지를 쉽게 파악할 수 있다.

이러한 변화는 Spectral envelop의 변화라고 한다.
(평탄했던 Spectral의 높낮이가 변함)

실제로 X와 Y의 소리를 듣게 되면 상당한 변화가 느껴진다고 한다.
교수님의 말씀으로는 이러한 Spectral envelop의 변화가 사람 음성에서는 발음을 결정하는 요소가 된다고 한다.

Z-Transform

h[n] 또는 H(f)는 시스템의 동작 구조를 효율적으로 보여주지는 못한다.
H(f)는 시스템을 쉽게 파악할 수 있게하지만, 여러번의 transform을 요구한다.

그래서 z-transform을 이용하여 시스템의 동작 구조를 쉽게 파악할 수 있게 한다.

위의 식에서 볼 수 있듯이, Z-Transform을 사용하면 쉽고 빠르게 어떤 동작이 이루어지는지를 파악할 수 있다.

H(z) = X(z) / Y(z) 라는 식에 초점을 맞춰보면, 분자는 인풋에 어떤 시스템이 적용되는지를 파악할 수 있고, 분모는 피드백이 어떤 식으로 들어가는지를 파악할 수 있다.

위는 Z-Transform을 이용하여 시스템의 동작 구조를 블록 다이어그램으로 표현한 그림이다.
이처럼 Z-Transform은 h[n]이나 H(f)보다 쉽게 시스템의 동작 구조를 이해하도록 해준다.